Dynamic Recursive API with F#
In this post I will implement a state machine using recursion and continuation functions. These two concepts enables us to implement a state machine with a dynamic recursive API that hides any data associated with states while enforcing the client to perform only valid transitions between the states.
Here is the complete code listing of this blog post.
But why?! Except being an interesting exercise, this is actually a very usable approach to implement any application that can be modelled as a state machine with some sort of actor. I use the word actor to mean someone or something that decides which transtions are made. For example all turn based games fall into this category. I’m indeed using this approach with a card game I’m currently working on. Scott Wlaschin has also written a very educational article where he uses this approach to implement Tic Tac Toe.
The idea of recursive API
What on earth is recursive API? It’s an API that is consumed recursively by the client. Duh! The idea is that instead of providing a static list of functions for the client, we provide possible actions based on previous action of the client. The only thing client code needs to do, is to choose from available actions which one to execute.
In object oriented code, state machine interface API could consist of a single method stateMachine.PerformTransitionTo(targetState), but not all states are valid inputs. In fact, what is valid input depends on the current state of the machine. To mitigate this problem, we could add another method to the API that would allow us to ask which are valid target states: List<State> validTargets = stateMachine.GetValidTargetStates(). Now the client code can first request valid target states and then choose one of them and pass it to PerformTransitionTo method. But why seprate these two things? Why not return functions immediately from GetValidTargetStates() instead of values that are passed back into the state machine by another method?
This is exactly what our recursive API will do. It returns a list of functions. Those functions represent all valid transitions that client code can make. Client code chooses one and executes it, resulting to a new list of functions to choose from and so it continues recursively until there are no valid transitions to make. To put it another way, when the end state has been reached.
State machine
Here is the state machine we will implement in this post.
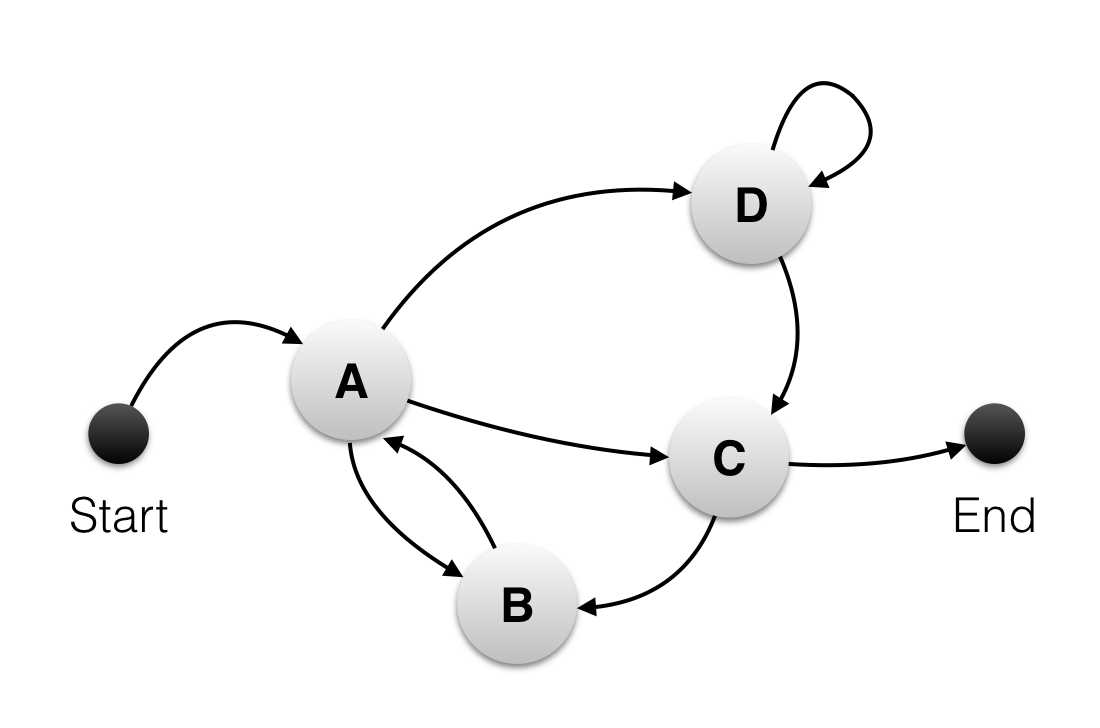
Let’s start by intoducing a type to enumerate all possible states of the system.
type State =
| StateA
| StateB
| StateC
| StateD
| EndEasy!
The next task is to model transitions (arrows in the picture) between the states. I will do this by implementing a function of type State -> State list, where the input is the source state and the output is all allowed destination states.
let transitions = function
| StateA -> [StateB; StateC; StateD]
| StateB -> [StateA]
| StateC -> [StateB; End]
| StateD -> [StateC; StateD]
| End -> []I find this to be readble representation of transitions. Notice how there are no transitions from the end state.
These two simple definitons allow us to represent the whole state machine by code. I don’t know about you, but I can’t think of more compact way to represent a state machine. F# syntax really shines here!
Next we will define types for the recursive API. These are the types that client code sees. API will return all possible valid transitions and the client code will execute one of those transitions. Let’s define a type Transition to represent transition option the client can perform. Transition consists of target state and continuation function that moves state machine into target state. We bundle target state with continuation function so that the actor knows what each function does. These Transitions are wrapped into TransitionResult that is returned as a result of each state transition.
type Transition =
{ TargetState: State
Continuation: unit -> TransitionResult }
and TransitionResult =
{ CurrentState: State
Transitions: Transition list }This is where the recursive nature of the API becomes visible. We need to use and keyword to define TransitionResult, because these two types depend on each other recursively. This raises a problem: How to instantiate a TransitionResult? We need to instantiate list of Transitions to be able to create TransitionResult, but in order to create Transition instances we need to create continuation functions that return TransitionResult instances. Seems like a chicken-egg problem! Circular dependency between these two types must be broken somehow. But how?
Here is my attempt to instantiate TransitionResult
let result =
{ CurrentState = StateA
Transitions = transitionsOf StateA }Not too difficult, but I used a function transitionsOf that we haven’t implemented yet! This imaginary function is able to create all valid transitions from StateA. If we are able to implement this function, we are done with the recursive API! Client could use result.Transitions to choose one of the transitions and execute it’s continuation function, which in turn would return a new result for the client and so on…
But how to solve the chicken-egg problem of recursive types? Unsurprisingly with a recursive function! But the real insight is that we can create those recursive dependencies lazily as the API is consumed. In other words, our recursive function is evaluated one step/loop at a time as the client code calls continuation functions.
Here is the implementation of the function with a signature State -> Transition list.
let rec transitionsOf state =
[for targetState in state |> transitions do
yield { TargetState = targetState
Continuation = fun () ->
{ CurrentState = targetState
Transitions = transitionsOf targetState }}]It’s only 6 lines of code, yet far from trivial function!
There are few aspects of this function that makes it difficult to grasp. The function returns a list of functions that are created at runtime as lambdas and each of those lambdas call the function itself recursively. It takes some time to sink in, so don’t worry! I recommend playing around with the code to really get it.
Finally we need a convenient way to start the state machine. For that purpose we implement a simple value called start. It’s just a TransitionResult record containing initial state, which in this case is a StateA. Here is the code:
let start =
{ CurrentState = StateA
Transitions = transitionsOf StateA }Now we have a fully functional dynamic recursive API for clients to consume. Next we will implement an actor and simple engine to illustrate how this API can be consumed.
Actor
Actor decides which transitions are performed. We define Actor as a record type to improve readability of our code. We could live without this type and just pass around function of type TransitionResult -> Transition, but I find it useful to communicate the concepts in code, thus the explicit Actor type.
type Actor =
{ DecideTransition: TransitionResult -> Transition }In order to instantiate an Actor, we need to implement one function of type TransitionResult -> Transition. This DecideTransition function takes in a result containing all the possible transitions. Reponsibility of the function is to choose one of those possible transitions and return it.
module Actor =
let random = System.Random ()
let decideTransition result =
let randomIndex = random.Next(result.Transitions.Length)
result.Transitions |> List.item randomIndex
let actor = { DecideTransition = decideTransition }This actor randomly chooses one of the transitions. In any real application we would implement a sopfisticated AI or some kind of UI to allow user to choose what happens next.
Engine
To utilize the state machine defined, we need an engine. It’s a recursive function that performs the transitions to the state machine based on the actor’s decisions. Here is the complete implementation of the engine.
module Engine =
let runWith actor =
let rec loop result =
if result.CurrentState = End then
()
else
let nextTransition = actor.DecideTransition result
nextTransition.Continuation () |> loop
start |> loopLet’s take a look at the code in more detail. First, we introduce a function runWith which takes an actor as a parameter. This function is merely a wrapper around the recursive inner function loop that does all the heavy lifting. The loop is a standard recursive function with a simple condition to check if it’s time to stop. If the current state is not the end state, it simply asks Actor to decide the next transition and then executes it. The result of the transition is piped to the loop recursively. Notice that the loop is a tail recursive function. This saves us from the stack overflow when dealing with long transition paths.
Let’s run it!
Now that we have all pieces in place we can simply run the state machine with our actor!
Engine.runWith actorYou can find the complete code listing from here. If you run it, you will quickly notice that you can’t see at all what happens. It just runs and stops. I recommend playing around with the code and adding printfn expressions in appropriate places to see how it acutally works.
What just happened?
We implemented a state machine with dynamic recursive API. I find this approach interesting for many reasons. First of all, we have no validation logic at all, even though it’s very strict which transitions can be made at all times. This is possible, because client code never inputs any parameters to our state machine. Instead those parameters are baked into functions we return as options for client to call.
It’s also notable that the whole codebase is immutable. We have no variables, yet we are modelling a state machine that inherently has a state. Immutablity enables us to execute these state machines parallel without any effort. This allows us to write AI for a state machine that can easily explore different paths parallel before deciding the transition. I find this approach to be a perfect fit for functional programming and turn based games.
Where to go from here?
Once you have a good intuition how this approach works you can start to extend it with things that real life applications usually need. Here are some exercises you could do:
- Add some data to each state. (For example count how many times each state was visited)
- Add another actor and modify the state machine so that those actors take turns
- Add some data to the
TransitionResultwhich allows actors to decide next transition based on pervious transitions. For example, in card game this data could contain cards on table that Actor is allowed to see. -
And last but not least, go and read the Scott Wlaschin’s blog post!